Overview

• Motivation
• The shift-share instrument
• Instrument validity: identifying assumptions
• Practical examples in literature
• Example in R

Motivation

Analysis of causal impacts within regional economic studies comes with challenges. It is often difficult to isolate true relationships between variables. Endogeneity issues are likely to arise, where the independent variable is correlated with the error term. This leads to biased coefficients in OLS regression.

Effect of immigration on unemployment

A typical question asked in economics is the impact of immigration on unemployment. This analysis seems straightforward with national panel data; if immigrants are substitutes for natives, immigration inflow is expected to raise unemployment. You would run the following regression:

\(UR_{i,t} = \beta_0 + \beta_1 IM_{i,t} + \beta_2 X_{i,t} + \epsilon_{i,t}\)

Where:

• $UR_{i,t}$ is the unemployment rate in region $i$, at time $t$
• $IM_{i,t}$ is the immigration inflow (from a specific origin country, or total immigration depending on your research question) to region $i$ in the destination country, at time $t$
• $X_{i,t}$ is a vector of controls, like variables for GDP growth or educational level in each region $i$, at time $t$
• $\epsilon_{i,t}$ is the error term

However, there is a concern with this regression design. If immigrants, seeking opportunities, are likely to gravitate towards regions with lower unemployment rates, immigration itself is driven by regional unemployment rates. This potential reverse causality creates an endogeneity problem.

The shift-share instrument

A shift-share instrument (also called the Bartik instrument) can be used to help solve this endogeneity issue. The shift-share IV decomposes changes in economic variables within regions into two components: the shift and the share. They are both assumed to be exogenous and together they can exogenously predict immigration inflows.

For the migration example, the instrument is a weighted average of predicted national immigration inflow rates (the shifts), with weights depending on the initial distribution of immigrants(the shares). In mathematical terms:

\(z_{i,t} = \sum_{i=1}^I s_{i,t-1} * m_{t}\)

Where:

• The share $s_{i,t-1}$: The lagged or “initial” distribution of the share of immigrants in the region $i$ (i.e. past settlement)

• The shift $m_{t}$: The national immigration inflow.

Note that the shifts vary at a national level and the shares at a regional level.

The regression model

The shift-share instrument $z_{i,t}$ is used to exogenously predict the endogenous shift (the immigration inflow into each region) in the following regression model:

\(UR_{i,t} = \beta_0 + \beta_1 z_{i,t} + \beta_2 X_{i,t} + \epsilon_{i,t}\)

Instrument validity

A crucial condition for the shift-share approach to work is instrument exogeneity. On average, the product of the instrument, $z_{i,t}$, and the error term $\epsilon_{i,t}$ should balance out to zero. In mathematical terms:

\(E[\frac{1}{I} \sum_{i} z_{i,t} \epsilon_{i,t}] = 0\)

Two recent perspectives in literature each highlight different assumptions for the shift-share instrumental approach to work: the share- and the shift-view.

Share-view

Goldsmith-Pinkham et al. (2020) show that the shares measure the differential exogenous exposure to the common shock (“shift”), while the shifts only provide the weights and do not affect the instrument endogeneity. Thus, the identifying assumption is: **shares $s_{i,t}$ are exogenous**, which is the following condition:

$E[\epsilon_{t} | s_{i,t} ] = 0$ for each $t$

In the migration example, this implies arguing whether the past settlement (initial distribution) of migrants can assumed to be uncorrelated with the local unemployment rates (the dependent variable).

Other assumptions

• Absence of spatial spillover effects

The absence of spatial spillovers means that the outcomes in one location are not influenced by the outcomes in neighboring regions, ensuring the independence of observations. This is not straightforward: If for example, domestic migration happens as a response to immigration inflow (native workers respond to immigration by moving to other regions), the negative effect of immigration on unemployment rates is likely to be overestimated.

• Independent data periods

The data represent distinct and independent periods without significant intertemporal correlations that might confound the estimation.

Shift (Shock) view

An alternative approach is introduced by Borusyak, Hull, and Jaravel (2022). This approach outlines identification arising from quasi-random shock assignment while allowing exposure shares to be endogenous. The two key assumptions are:

• Quasi-random shift assignment

$E[m_{t} | \bar{\epsilon}, s] = \mu$ for all $t$

Each shift has the same expected value, conditional on the shift-level unobservables $\bar{e_{t}}$, and average exposure $s_{t}$.

• Many uncorrelated shifts

This condition implies that when there are many regions, the shifts in different regions are becoming increasingly uncorrelated to each other. In other words, the covariance between the shifts in one region and the shifts in another region becomes close to zero when comparing different regions:

$Cov(m_t, m_t' | \bar{\epsilon}, s) = 0$ for all $m' \neq m$

Practical examples in literature

Several studies demonstrate the application of the shift-share instrument in various economic contexts.

Note: The instrument is $z_{l} = \sum_{n} s_{l,n} * m_{n}$ where shifts (shocks) vary at another level (n) than the shares (l), and outcome and treatment are observed at level l.

Context	Shift-Share Instrument	Authors
Employment impact on wage growth in region l	Predicted employment due to national industry trends Shifts: National growth of industry n Shares: Lagged employment shares of industry in region l	Bartik (1991); Blanchard & Katz (1992)
Local labor market effects of rising Chinese import competition in the US	Predicted growth of import competition Shifts: Growth of China exports in manufacturing industry n Shares: 10-year lagged employment shares over total employment in region l	Autor, Dorn, and Hanson (2013)
Import impact by Danish firm on wages	Predicted change in firm inputs via transport costs Shifts: Changes in transport costs by n = (product, country) Shares: Lagged import shares	Hummels et al. (2014)

Example in R

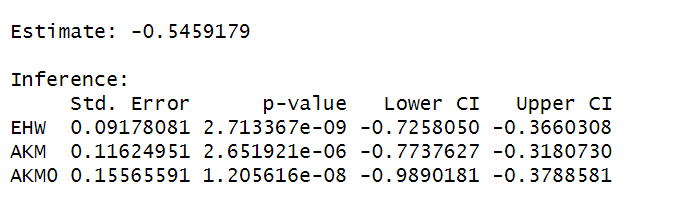
This R code illustrates the estimation of the second literature example from Autor, Dorn, and Hanson, (2013), using the ShiftShareSE package and the data set (ADH), which is included in the package.

The ivreg_ss() function is used to estimate a regression model with the shift-share instrument.

The code contains the following terms:

• d_sh_empl is the dependent variable; the change in the share of the working-age population.
• No controls are added, thus the controls term equals 1.
• shock is the endogenous regressor and represents the local China imports.
• The instrument used to replace shock is IV. This is the shift-share vector, with length N of sectoral shocks, aggregated to the regional level using the share matrix W.
• W is a matrix of sector shares (the weights).
• method specifies which inference methods to use.