Overview

When training a machine learning model, we use an optimization approach to minimize a cost function. Gradient descent serves as a crucial optimization method for optimizing weights in cost functions during regression and classification tasks. This article aims to provide insights into selecting the best optimization algorithm and pairing it with the appropriate loss function when training a machine learning model.

It is highly recommended to review the Cost and Loss Functions article before reading this article.

Optimization

In the context of machine learning and mathematics, optimization involves finding the best possible solution or configuration for a given problem. This often includes minimizing or maximizing an objective function by adjusting the parameters or variables of a model or system. Feel free to explore more by reading this paper. In mathematics, various optimization algorithms exist. One of the most common methods, particularly in machine learning, is known as Gradient Descent(GD).

Gradient descent algorithm in simple language

Imagine you’re trying to predict house prices based on their sizes. You have a dataset with the sizes of houses $x(i)$ and their corresponding prices $y(i)$. You want to build a model that can accurately predict house prices based on their sizes.

Equation 1 represents the hypothesis function $h_\theta(x)$, which predicts the house price ($y$) based on its size ($x$). In this case, $\theta_0$ is the intercept term (representing the base price of a house) and $\theta_1$ is the coefficient that represents how much the price of a house increases per unit increase in size.

Now, let’s consider Equation 2, which represents the cost function $J(\theta_0, \theta_1)$. This function calculates the difference between the predicted house prices ($h_\theta(x)$) and the actual prices ($y$), squared and averaged over all the data points. The goal of gradient descent is to minimize this cost function by adjusting the parameters $\theta_0$ and $\theta_1$.

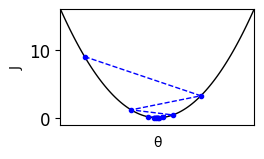
To do this, the gradient descent algorithm starts by initializing $\theta_0$ and $\theta_1$ with random values. Then, it iteratively updates these parameters using the formula:

When optimizing your machine learning algorithm, it’s crucial to consider the learning rate, denoted here as $\alpha$. It controls the size of the steps taken during optimization. Let’s say we start with $\alpha = 0.01$.

In each iteration, the algorithm computes the partial derivatives of the cost function with respect to $\theta_0$ and $\theta_1$, scales them by $\alpha$, and updates the parameters accordingly. This process continues until the cost function converges to a minimum.

However, choosing the right learning rate is crucial. If the learning rate is too large, the algorithm may overshoot the minimum and fail to converge. Conversely, if it’s too small, the algorithm may take too long to converge.

Let’s say we experiment with different learning rates: $\alpha = 0.1$, $\alpha = 0.01$, and $\alpha = 0.001$. We visualize their effects on the convergence of the cost function in the graph.

By fine-tuning the learning rate and monitoring the convergence of the cost function, we can optimize our machine learning algorithm to make accurate predictions of house prices based on their sizes.

Gradient Descent Variants

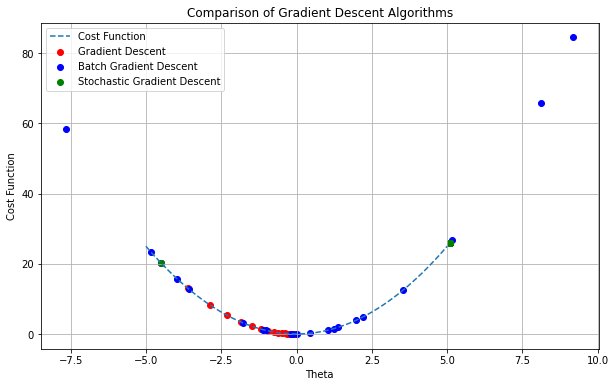
Various variants of Gradient Descent exist, such as batch gradient descent, stochastic gradient descent. While the fundamental concepts remain consistent across these variants, the approach each algorithm adopts to solve the optimization problem differs.

Batch Gradient Descent (BGD)

In gradient descent, during each iteration, the parameters of the cost function ($\theta_i$) are updated simultaneously for a single sample point. However, in BGD, a single step involves considering the entire training dataset. The model parameters are updated by calculating the average of gradients from all training samples, using this mean gradient for updating. This involves a single iteration of gradient descent within one epoch.

Advantages:

• BGD is particularly suitable for convex problems, such as the Sum of Squared Errors (SEE) cost function.
• It offers high accuracy

Disadvantages:

• As expected, this algorithm tends to be slow on large datasets.
• It requires more computation and memory, as it considers all training samples at once.

Stochastic Gradient Descent(SGD)

Named “stochastic” due to its approach, the algorithm randomly selects one training sample in each iteration to calculate the gradient. This means the algorithm employs either a single sample entry or a small set of training samples to compute the gradient, optimizing the weights. However, since each iteration adjusts the weights using a randomly chosen sample, the cost fluctuates, and it may not consistently decrease.

Advantages:

• The convergence speed of this algorithm surpasses that of BGD, making it particularly suitable for nonconvex problems like the L1 loss function.
• In the case of very large datasets, SGD is preferred over BGD, as BGD processes the entire dataset in every iteration. However, for implementing SGD, it is recommended to use a set of training data rather than a single instance.

Disadvantages:

• There is a possibility that the algorithm doesn’t always reach the minimum but fluctuates around it. It is important to note that with a sufficient number of iterations, the overall trend of the cost tends to decrease.

Mini Batch Gradient Descen(MGD)

This algorithm presents a hybrid approach, blending aspects of both BGD and SGD. Unlike SGD, which involves selecting a single sample, and BGD, which considers the entire dataset, this variant of Gradient Descent operates on a fixed-length batch of training samples. By combining elements of the aforementioned algorithms, it leverages the advantages of both. In each iteration, a batch of samples is randomly chosen, and after computing the gradient on these samples, the average gradient is employed to update the weights of the cost function. It’s worth noting that fluctuations may occur due to the use of a relatively small group of samples in each iteration.

Advantages:

• One key benefit of MBD compared to SGD is the potential performance enhancement achieved through hardware optimization of matrix operations.
• This algorithm is favored for optimization in deep learning due to its ability to balance speed and stability effectively.

Disadvantages:

• Convergence of an error cannot be assured with certainty.
• Manually regulate the learning rate when employing MGD. If the learning rate is set too low, the convergence rate may decrease. Conversely, if the learning rate is too high, it may lead to failure in getting an absolute global or local minimum. Thus, careful control of the learning rate is essential in MGD.

The image below shows the distinctions among three variants of Gradient Descent.

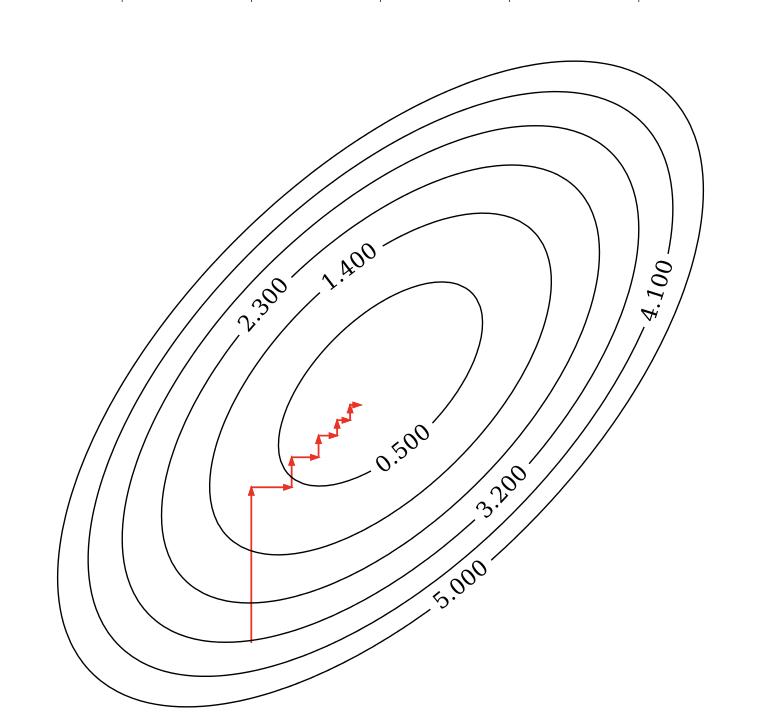
Coordinate Descent(CD)

CD optimizes one variable at a time while cycling through the entire set of variables repeatedly. The method optimizes a single coordinate in each iteration by determining the minimum along that specific coordinate while keeping others constant. Following that, the process continues with another coordinate, often employing a selection rule like round robin.

-

Advantages:

• It is applicable for convex loss functions that lack differentiability, such as those encountered in Lasso regression.
• This technique highlights faster iterations and bypasses the necessity to manually choose a learning rate

Disadvantages:

• It may exhibit slower convergence compared to gradient descent.
• A notable limitation is its non-parallelizable nature, restricting its effectiveness in parallel computing settings.