What is Deep Learning?
Deep learning is a type of machine learning that's inspired by the structure and function of the human brain, particularly in how it processes information and learns from it. It's called "deep" learning because it involves neural networks with many layers—these are the "deep" part. Each layer of these networks learns to transform the data in a way that makes it more useful for achieving the network's overall goal.
Deep learning is commonly used in image recognition, natural language processing, and speech recognition tasks. It finds applications in industries such as healthcare, finance, and autonomous vehicles, where it enables tasks like medical diagnosis, fraud detection, and autonomous driving.
Neural Networks: Inspired by the Brain
Deep learning draws inspiration from the human brain's complex structure. Geoffrey Hinton's pioneering research asked: Can computer algorithms mimic brain neurons? This exploration aimed to harness the brain's power by mirroring its architecture. The anatomy of a single neuron is presented below.
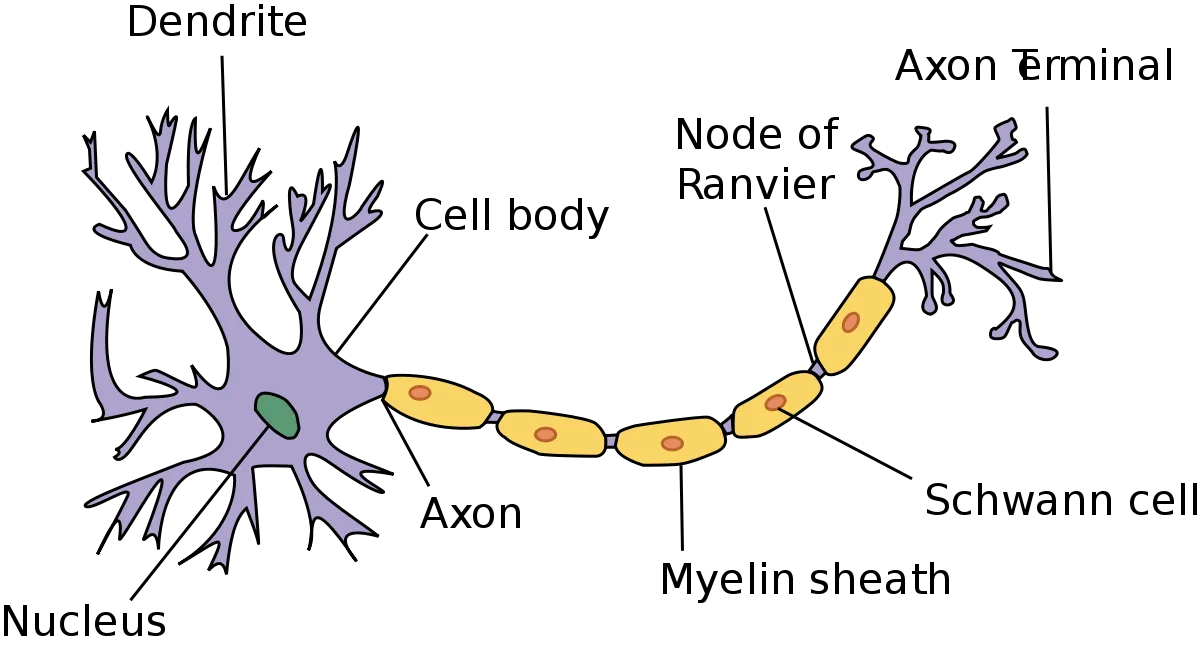
Picture source: McCullum, N. (2021, 28 april). Deep Learning Neural networks explained in Plain English
Neurons, the brain's building blocks, work in networks, where their combined activity creates meaning. Neurons receive and send signals through dendrites and axons. In computer models, this is replicated through weighted inputs and activation functions.
Mimicking Neurons in Computers
In deep learning, neurons gather inputs, compute weighted sums, and pass them through activation functions. Weights, vital for model training, adjust to optimize performance, forming the core of deep neural network training.
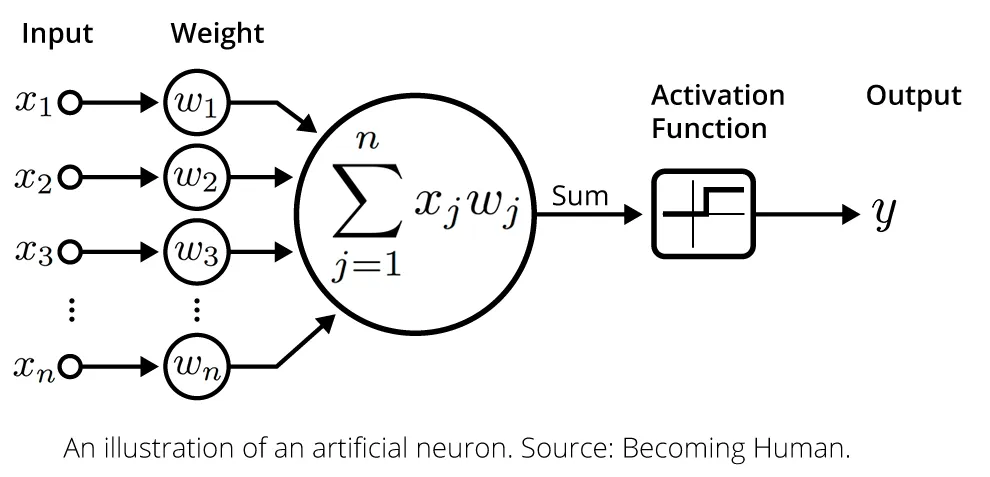
Picture source: McCullum, N. (2021, 28 April). Deep Learning Neural Networks Explained in Plain English.
Shallow and deep neural networks
Neural networks could be distinguished between shallow and deep neural networks. What is the difference?
Single-layer neural networks, also referred to as shallow neural networks, comprise a single hidden layer positioned between the input and output layers. This hidden layer conducts computations, orchestrating the transformation of input data to yield the intended output. Shallow neural networks, though straightforward, possess restricted capacity for learning intricate patterns and representations.
In contrast, deep neural networks boast multiple hidden layers distributed between the input and output layers. These networks can be profoundly deep, incorporating tens or even hundreds of layers. Each layer undertakes computations, forwarding the modified data to the subsequent layer in succession.
Components of deep learning network
In the sections above we introduced concept of deep learning and we talked a little bit about biology behind it. Let's move now to explaining separate components of deep learning architecture.
-
Input layer refers to the first layer of nodes in an artificial neural network. This layer receives input data from the outside world.
-
Hidden layers are what make neural networks "deep" and enable them to learn complex data representations.
-
Output layer is the final layer in the neural network where desired predictions are obtained. There is one output layer in a neural network that produces the desired final prediction.
How information is transferred between the layers?
In neural networks, information is transferred between layers through weighted connections. Each neuron in a layer receives input from neurons in the previous layer, multiplies these inputs by corresponding weights, sums them up, and applies an activation function to produce an output. This output becomes the input for neurons in the next layer, and the process repeats for each layer until reaching the output layer.
Loss function
The loss function in deep learning measures how well the model's predictions match the actual targets in the training data. It quantifies the difference between predicted and true values, providing feedback for adjusting the model's parameters during training. The goal is to minimize the loss function, indicating better alignment between predictions and actual outcomes, ultimately improving the model's performance.
Mathematically speaking the loss function is the chosen family of mathematical equations which returns a scalar that is smaller when the model maps inputs to outputs better.
$L[\theta, f[x, \theta], { [x_{i}, y_{i}] }^{I}_{i=1} ]$
where:
-
$ f[x, \theta] $ is a deep learning model
-
${ [x_{i}, y_{i}] }^{I}_{i=1}$ is a training data
Training process
Let us denote our training dataset of I pairs of input/output examples:
$\text{Training Data: }$ ${ [x_{i}, y_{i}] }^{I}_{i=1}$
Training consists in finding the model's parameters to minimize the loss function, i.e:
$\hat{\theta} = argmin[L[\theta, f[x, \theta], { [x_{i}, y_{i}] }^{I}_{i=1}]]$
A single prediction $\hat{y}$ can be denoted in the following way:
$\hat{y} = f[x, \hat{\theta}]$
Activation function
Activation functions are essential components of neural networks as they introduce nonlinearity, a crucial element for enabling the development of intricate representations and functions. This nonlinearity expands the network's capacity to capture complex relationships and patterns from the inputs, surpassing the capabilities of a basic linear regression model.
Multiple options are available for the choice of the activation function:
-
Sigmoid function (only used in the output layer of the logistic regression): $ a(z) = \frac{\mathrm{1} }{\mathrm{1} + e^-{z} } $
-
Tanh function: $ a(z) = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}} $
-
ReLU function: $ a(z) = \max(0,z)$
Optimizer
An optimizer in the training process of a neural network is like a guide that helps the network learn from the data more effectively. Its main job is to adjust the model’s parameters (like weights and biases) so that the predictions get closer to the actual targets over time. This adjustment is informed by the gradients of the loss function, which indicate the direction of steepest ascent or descent in the parameter space. By iteratively updating the parameters based on these gradients, the optimizer guides the network towards minimizing the loss and improving its predictive accuracy.
Mathematical representation
After introducing all necessary concepts, lets take a look how layers are represented mathematically: First let's consider very small neural network which has only 2 hidden layers:
$\small \text{Inputs: } { x_{i} }^{I}_{i=1}$
$ \small \text{$1st$ hidden layer: } h_{0} = a[\beta_{0} + \Omega_{0}x] $
$ \small \text{$2nd$ hidden layer: } h_{1} = a[\beta_{1} + \Omega_{1}h1]$
$ \small \text{Output layer: } y = \beta_{2} + \Omega_{2}h_{2} $
This small neural network, mathematically would be denoted in the following way:
Moving now to more general formula with k number of hidden layers.
$ \small \text{Inputs: } { x_{i} }^{I}_{i=1}$
$ \small \text{$kth$ hidden layer: } h_{k} = a[\beta_{k-1} + \Omega_{k-1}h_{k-1}] $
$ \small \text{Output layer: } y = \beta_{k} + \Omega_{k}h_{k} $
where: - $a$ is an activation function - $\beta$ is bias vector (biases: additional parameters added to the weighted sum before applying the activation function) - $\Omega$ is a weight matrix (grid-like structure containing numerical values. Each value in the matrix represents the strength of a connection between neurons in one layer and neurons in the next layer of a neural network.)
Finally the general equation of the deep neural network could be annotated as following:
Graphical represantion of a deep neural network:
This is how deep neural network could be presented in the graph:
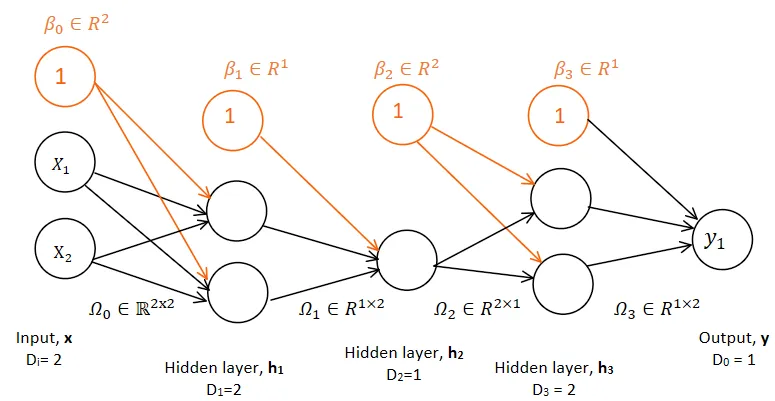
Coding deep neural network
Coding deep neural networks involves using programming languages such as Python, which is highly popular due to its simplicity and extensive libraries for machine learning and neural networks. Libraries like TensorFlow and PyTorch are widely used for building and training deep neural networks, providing high-level APIs for constructing complex architectures with ease.
Building and training deep neural networks involves several steps, including loading and preparing the data, constructing the model architecture, and compiling, fitting, and evaluating the model. In this section, we will break down each of these steps in detail.
Loading and Preparing the Data
In this section, we load the MNIST dataset and preprocess it for training and testing.
We begin by importing necessary libraries for data manipulation and preprocessing. Then, we load the MNIST dataset using Keras' built-in function mnist.load_data(). The dataset consists of 60,000 training images and 10,000 test images, each with their corresponding labels. Next, we preprocess the data by reshaping the input images and normalizing pixel values to a range between 0 and 1. Additionally, we convert the class labels to categorical format using one-hot encoding.
import numpy as np
from keras.datasets import mnist
from keras.utils import to_categorical
# Load the MNIST dataset
(X_train, y_train), (X_test, y_test) = mnist.load_data()
# Preprocess the data
X_train = X_train.reshape((X_train.shape[0], -1)).astype('float32') / 255
X_test = X_test.reshape((X_test.shape[0], -1)).astype('float32') / 255
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
Building the model
In this section, we construct the neural network model using Keras' Sequential API.
We create a Sequential model, which allows us to build a linear stack of layers. The model consists of dense (fully connected) layers, which are interconnected neurons. Each dense layer performs a linear operation on the input data followed by a non-linear activation function. In our model, we use ReLU (Rectified Linear Activation) as the activation function for hidden layers and softmax for the output layer. The units parameter specifies the number of neurons in each layer, and input_shape defines the shape of the input data for the first layer.
from keras.models import Sequential
from keras.layers import Dense
# Creating a Sequential model
model = Sequential()
# Adding layers to the model
model.add(Dense(units=64, activation='relu', input_shape=(X_train.shape[1],)))
model.add(Dense(units=64, activation='relu'))
model.add(Dense(units=10, activation='softmax'))
Compiling, fitting and evaluating the model
In this section, we compile the model with an optimizer, loss function, and evaluation metric, train the model on the training data, and evaluate its performance on the test data.
After building the model, we compile it using the compile() method. Here, we specify the optimizer (Adam), loss function (categorical cross-entropy), and evaluation metric (accuracy). Then, we train the model on the training data using the fit() method, specifying the number of epochs (iterations over the entire dataset) and batch size (number of samples per gradient update). Finally, we evaluate the trained model on the test data to measure its performance in terms of loss and accuracy.
# Compiling the model
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
# Training the model
model.fit(X_train, y_train, epochs=10, batch_size=128, verbose=1, validation_split=0.2)
# Evaluating the model
loss, accuracy = model.evaluate(X_test, y_test, verbose=0)
print("Test Loss:", loss)
print("Test Accuracy:", accuracy)
 Summary
SummaryWhat is Deep Learning?
Deep learning is a branch of machine learning inspired by the structure and function of the human brain. It involves the use of neural networks with multiple layers to process and learn from data. The term "deep" refers to the depth of these networks, which enable them to extract complex patterns and representations from the data.
Mimicking the Behavior of Neurons in Computer Algorithms**
Deep learning aims to mimic the behavior of neurons in the human brain through computer algorithms. Researchers study the collaborative nature of neurons and replicate it in artificial neural networks. This involves computing the weighted sum of inputs, applying activation functions, and transmitting signals between layers to process information.
Architecture of Deep Neural Networks
Deep neural networks consist of multiple layers, including input, hidden, and output layers. Information flows through the network via weighted connections between neurons in adjacent layers. The architecture allows for the hierarchical extraction of features from raw data, with each layer learning increasingly abstract representations.
Components of deep neural networks
The training process involves optimizing the model's parameters to minimize a loss function, which measures the disparity between predicted and actual values. Activation functions introduce nonlinearity to the network, enabling it to capture complex patterns. Practical implementation also includes data preprocessing, model compilation, and evaluation using libraries like TensorFlow and Keras in Python.
Practical Implementation in Python
Python is a popular choice for practical implementation of deep learning models due to its simplicity and extensive libraries. TensorFlow and Keras are commonly used libraries for building and training deep neural networks. Practical implementation involves data preprocessing, defining the model architecture, compiling the model, training it on the data, and evaluating its performance.
References:
Prof. Matteo Bustreo, 2024 “Lesson2-Foundations of Deep Learning" https://tilburguniversity.instructure.com/courses/14887/files/2934299?module_item_id=669643.
McCullum, N. (2021, 28 april). Deep Learning Neural networks explained in Plain English. freeCodeCamp.org. https://www.freecodecamp.org/news/deep-learning-neural-networks-explained-in-plain-english/





