Introduction
Difference-in-differences (DiD) and event study designs are among the most popular quasi-experimental approaches used in empirical research in economics and the social sciences. The fundamental identification assumption behind these methods is the parallel trends assumption (also referred to as the common trends assumption). This assumption entails that, in the absence of treatment, the two groups would have followed similar (i.e., parallel) trends in the outcome. Of course, we do not observe what would have happened had treatment not been implemented, so this assumption is not fully empirically verifiable. However, researchers often present evidence that the groups followed parallel trends before the treatment was introduced to lend credibility to the DiD or event study design they are using.
 Tip
TipThis topic is about the design and shortcomings of commonly used tests for the parallel trends assumption. For an alternative approach to DiD that addresses these problems, see Honest DiD.
Testing for pre-trends
Testing for the statistical significance of differences in pre-trends between groups, i.e. the trends prior to the treatment introduction, is one popular way of checking the validity of the parallel trends assumption. If we do not observe any statistically significant difference in these pre-trends, we tentatively conclude that the parallel trends assumption holds. Conversely, if significant differences are present, we may have to re-consider the validity of our design or use a version of DiD that does not require the assumption to hold (see the 'Recommendations' section below).
In practice, in a DiD or event study setting, we will often have multiple pre- and post-treatment periods. For example, we might measure the outcome 4 years before and 4 years after the treatment is implemented. A test for pre-trends would then imply testing for differences between the treatment and control groups in each of the 4 years before the treatment. We could then use two criteria for assessing the validity of the parallel trends assumption: 1. Individual significance of the coefficients: we consider the assumption valid if and only if none of the 4 differences is statistically significant. 2. Joint significance of the coefficients: We consider the assumption valid if the 4 differences are not jointly statistically significant.
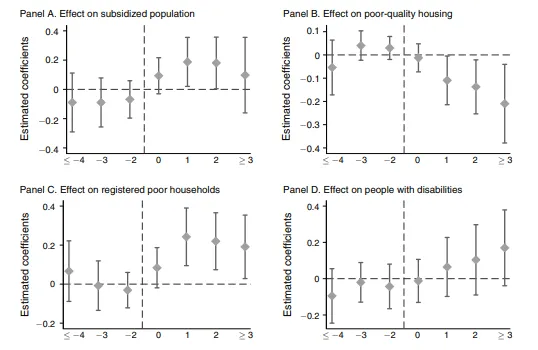
He and Wang (2017) study the effect of the allocation of so-called college graduate village officials (CGVOs) to rural communities in China on poverty alleviation. CGVOs are assigned bureaucratic roles in villages to help local governments successfully implement the central government’s anti-poverty policies. The idea behind the policy is that college graduates should be more able and efficient administrators than rural government leaders. They use a staggered difference-in-differences design, exploiting the fact that CGVOs were allocated to villages in a staggered (gradual) fashion. For example, village A might have been assigned a CGVO in 2001, village B in 2004, and village C in 2005. They test for the parallel trends assumption by testing for the statistical significance of between-group differences in their four outcomes of interest for each of the pre-treatment periods they have in their sample:

They also present graphical evidence of the validity of their common trends assumption, shown in this event study plot:
Problems with common tests for pre-trends
Significance tests and event study plots are straightforward and intuitive ways of testing for the validity of the parallel trends assumption. However, they are subject to some notable shortcomings, which are discussed in detail by Roth (2022). We look at the two main shortcomings below: low statistical power and exacerbation of bias.
Low statistical power
The first major problem with the conventional tests for pre-trends is that they often have low statistical power. Statistical power is a measure of how likely we are to find a statistically significant effect (or difference) if there is one, given the characteristics of our design, such as sample size, the significance level, and the minimum effect size we want to be able to detect.
Low statistical power essentially means that we will not detect statistically significant differences in pre-trends unless they are very large. This is problematic because small or medium differences can also pose a threat to the parallel trends assumption and thus to reliable causal inference in DiD and event study settings.
 Tip
TipRead more about statistical power and the problems associated with low statistical power here.
Going back to the He and Wang (2017) paper, let’s imagine that there are differences in trends between the treated and untreated villages before the treatment is introduced. For example, the trend in poor housing is already decreasing in the treated villages, while in untreated ones it is not. However, the test we use to check for parallel trends has lower power and we are unable to detect this difference, so we assume that the parallel trends assumption holds and proceed to estimate the treatment effect. We find that the difference in differences is negative, that is, the treatment has apparently decreased the share of poor housing. Since the trend before the treatment was introduced was already like this, we cannot attribute this observed difference to the treatment, but we do not know this because low statistical power impedes the detection of the pre-treatment difference in trends. In this way, using low-powered pre-trend tests to verify the parallel trends assumption can lead to mistaken causal inference.
Low statistical power is not a problem exclusive to tests for pre-trends: it also often occurs with the estimation of the treatment effects of interest. However, it can occur more frequently with pre-trend tests due to lower sample sizes (if we are looking at each pre-treatment period separately) and higher levels of noise in the outcome before treatment is implemented. In any case, it is always useful to assess the power our pre-trends test has to evaluate its capacity to detect significant differences in pre-trends and establish the credibility of the parallel trends assumption.
We can do this using the pretrends package in R.
We first install and load the package into R using the code below.
#install and load the pretrends package
install.packages("remotes")
remotes::install_github("jonathandroth/pretrends")
library(pretrends)
The package contains some data from He and Wang's (2017) paper, which we discussed above. In this example, we will work with these data, but the functions of the pretrends package can be easily applied to any other DiD or event study estimation.
#define the variables by loading them from the pretrends package;
#these are based on the paper by He and Wang (2017)
beta <- pretrends::HeAndWangResults$beta #vector of He and Wang's treatment coefficient estimates for each time period
sigma <- pretrends::HeAndWangResults$sigma #variance-covariance matrix of the main regression of He and Wang's study
tVec <- pretrends::HeAndWangResults$tVec #vector of time periods
referencePeriod <- -1 #define the last period before treatment
 Tip
TipIn order to get the variance-covariance matrix of your regression, use the vcov() function in R, or the vcovHC() or vcovHAC() functions from the sandwich package for heteroskedasticity- and heteroskedasticity and autocorrelation-consistent standard errors, respectively. Supply the variable name of your model as the argument.
The package allows us to determine the minimum size of the difference in pre-trends that we would be able to detect given a certain level of power. We use 80% power - the gold standard in the social sciences.
#this function gives us the minimum size of the violation of the parallel trends assumption
#we could detect given a certain level of power (80% in this example)
trend80 <- slope_for_power(sigma = sigma, #define the variance-covariance matrix
targetPower = 0.8, #choose our target power
tVec = tVec, #define the vector of time periods
referencePeriod = referencePeriod) # define the reference period
trend80
Output

This result means that we can detect a difference in pre-trends of 0.079 (3 decimal points; dp) 80% of the time. We will be able to detect larger differences more frequently and smaller differences less frequently. This result also clearly illustrates the problem with low-powered pre-trends tests - if we had a difference in pre-trends of 0.05, for example, which is still sizeable, we would detect it less than 80% of the time with our test. We can compute the exact power we would have for a difference of 0.05 using the pretrends function of the pretrends package:
#this function allows us to calculate the power to detect
#a violation of parallel trends of a given size (0.05 in this example)
pretrendsResults <-
pretrends(betahat = beta, #define variables as previously
sigma = sigma,
tVec = tVec,
referencePeriod = referencePeriod,
deltatrue = 0.05 * (tVec - referencePeriod)) #define the size of the violation of the parallel trends assumption (0.05 in our example)
pretrendsResults$df_power #compute power
Output

We see that we would only be able to detect a difference in pre-trends of 0.05 47.5% (1dp) of the time. Our pre-test is clearly flawed - in more than half of the cases, we would be unable to establish a violation of the parallel trends assumption if this violation were a 0.05-point diffence in the pre-treatment trends in the outcome variable between the treatment and control groups.
Exacerbation of bias
Another problem with testing for pre-trends by evaluating the significance of pre-treatment differences in the outcomes is that pre-trends themselves can exacerbate the bias in the estimated treatment effect when there are meaningful differences between the two groups prior to the treatment (i.e., when the parallel trends assumption is violated).
Let’s assume that, in our setting, the parallel trends assumption is violated, that is, there is a significant difference in pre-trends between the treatment and control groups. We run a pre-trend test before proceeding to estimating the treatment effect. Say that our test has 60% power, then we will detect the difference in pre-trends 60% of the time. We can condition our estimation of the treatment effect on the pre-trend test being passed (i.e., no difference being observed) – in that case, we only estimate the treatment effect in the 40% of cases where we do not detect a discrepancy in pre-trends. This 40% of cases will inevitably contain smaller pre-trend differences, as these are more difficult to detect. We can see how this leads to greater bias with a very simplified stylised model of bias in a DiD/event study setting:
 Example
ExampleWe define $\hat{\beta}$ as our estimate of the treatment effect, which is composed of the estimated difference between the treatment and control groups after treatment implementation, $\hat{\beta_{post}}$, and the corresponding difference before treatment implementation, $\hat{\beta_{pre}}$.
$\hat{\beta} = \hat{\beta_{post}} – \hat{\beta_{pre}}$
Analogously, we define $\beta$ as the true treatment effect.
$\beta = \beta_{post} – \beta_{pre}$
Finally, we define bias, $\delta$, as the difference between the estimator and the true effect.
$\delta = \hat{\beta} - \beta$
Let's suppose that the true differences before and after treatment are 5 and 10, respectively; hence, the true effect is 10.
$\beta = 10 - 5 = 5$
Now let's suppose that the parallel trends assumption is violated in the true model. We conduct a test for pre-trends and only proceed to estimate treatment effects if the test is passed. With our power of 0.6, we only detect the violation 60% of the time; let's assume that in the 40% of cases where we do not detect the difference (i.e., the 40% of cases with the smallest difference) the pre-treatment difference is 2. Therefore, our estimated effect is:
$\hat{\beta_{1}} = 10 - 2 = 8$
Consequently, the conditional bias with respect to the true effect is:
$\delta_{1} = \hat{\beta_{1}} - \beta = 8 - 5 = 3$
Now, let's suppose that we estimate treatment effects unconditionally, that is, regardless of whether we detect a difference in pre-trends or not using our test. The pre-trends difference that we will find in this case will certainly be higher than if we had estimated treatment effects conditionally as above; for example, 4. Our treatment effect estimate will therefore be:
$\hat{\beta_{2}} = 10 - 4 = 6$
Accordingly, the unconditional bias will be:
$\delta_{2} = \hat{\beta_{2}} - \beta = 6 - 5 = 1$
This example shows that, in a context where the parallel trends assumption is likely to be violated, conditioning our analysis on passing a pre-trend can result in greater bias in our estimators.
Recommendations
Below are some best practices to apply to deal with the limitations of pre-trend tests:
-
It is always useful to understand what level of statistical power the test that we are using has to be able to gauge its ability to detect actual violations of the parallel trends assumption and to judge whether conditioning our estimation of the treatment effect on the design passing a pre-trends test is likely to lead to higher bias in the estimated treatment effect. The
pretrendsR package, an example of the use of which is included above, is a handy tool for this purpose. -
Applying economic theory and intuition to our particular context is essential to assessing the likelihood of a violation of the common trends assumption. This also helps us understand to what extent the use of high-power pre-trends tests together with conditional treatment effect estimation can result in exacerbated bias. If the assumption is very likely to be contravened in our setting, conditioning our analysis on the assumption being passed will imply that we only look at extreme cases where the margin of the violation is very small, leading to large biases in the estimation of the treatment effect.
-
Recent econometric literature on DiD and event studies has proposed a number of solutions that circumvent the parallel trends assumption altogether. One such method is the so-called honest DiD approach developed by Rambachan and Roth (2023), where identification is valid as long as we can credibly established a set of restrictions $\Delta$ on the size of the difference in pre-trends between the treatment and control groups. Another is the method proposed by Freyaldenhoven et al. (2019), which uses a covariate affected by potential relevant confounders but not the treatment itself coupled with two-stage least squares (2SLS) to estimate treatment effects in an event study/DiD setting without regard for the validity of the parallel trends assumption.
Summary
 Summary
Summary- Conventional tests for pre-trends in DiD or event study settings are easy to apply and appear to directly address the fundamental identification challenge in such designs: establishing the credibility of the parallel trends assumption. However, such tests can be problematic for two reasons.
- Firstly, they often have low statistical power, making them relatively unlikely to detect violations of the assumption even when it is actually violated.
- Secondly, even when the tests are high-powered, conditioning the estimation of the treatment effect on a successful pre-trend test can result in exacerbated bias in our treatment effect estimator when there is a true violation of parallel trends.
- To avoid these issues, we can apply one of the newly proposed approaches to causal inference in DiD and event study settings which do not rely on the parallel trends assumptions, such as the honest DiD approach (Rambachan & Roth, 2022) or the covariate-instrument approach (Freyaldenhoven et al., 2019).
See Also
Pretest with Caution: Event-Study Estimates after Testing for Parallel Trends - Roth (2022)





